CompStor®
Accelerated Bioinformatic Algorithms and
Analytics Tools
Welcome to
CompStor®
CompStor® is a family of life science compute solutions for genomics and scientific computing. CompStor Novos® enables accelerated de novo assembly based variant calling. CompStor Analytics™ enables multi-terabyte machine learning applications.
We turn servers into supercomputers!

>1,000,000,000
reads in a WGS
High coverage, short-read
whole genome sequencing
>10,000,000 individual
genomes being sequenced
Ongoing global whole genome
sequencing efforts
De novo assembly and reference alignment based variant calling
CompStor Novos™ ready with 1-3 hour analysis times and precisionFDA winning accuracy results
CompStor Novos® Solution
CompStor Novos® Whole Genome Variant Calling
Accelerated compute enables both reference alignment and de novo assembly genome reconstruction methodologies. CompStor Novos' alignment pipeline produces highly accurate results for short variants - single nucleotide and indels (insertions-deletions). The de novo assembly pipeline contains larger structural variants not detectable with reference alignment techniques. Both methods are available on one accelerated appliance solution.
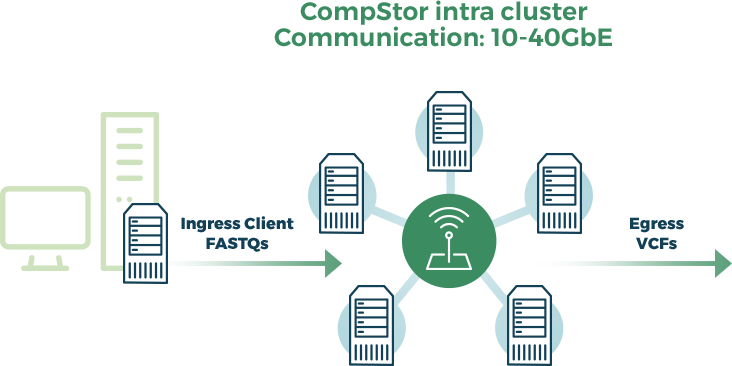
Bringing together
computation & storage

De novo assembly and reference alignment variant calling with precisionFDA winning results (>.999 F-score)

Multi-terabyte CBCL ⇒ FASTQ conversion and demultiplexing in under 30 minutes

2 or 4 node configuration

Optimized data ingress & egress
Analytics & Future Development
 Accelerate algorithms fundamental to AI, DL/ML, and Scientific Computing in TB sized formats
Accelerate algorithms fundamental to AI, DL/ML, and Scientific Computing in TB sized formats
- • Singular Value Decomposition
- • Principal Components Analysis
- • t-Distributed Stochastic Neighbor Embedding (t-SNE)
- • Eigen Analysis
- • Linear Regression
- • Markov Chains
- • Variance Analysis
 Pursuing collaborations and product development in
Pursuing collaborations and product development in
- • Fundamental disease characterization using Big Data
- • Multi-omic matrix calculations in terabyte scale datasets
- • Deep learning pathology image classification
- • Mass spec proteomics
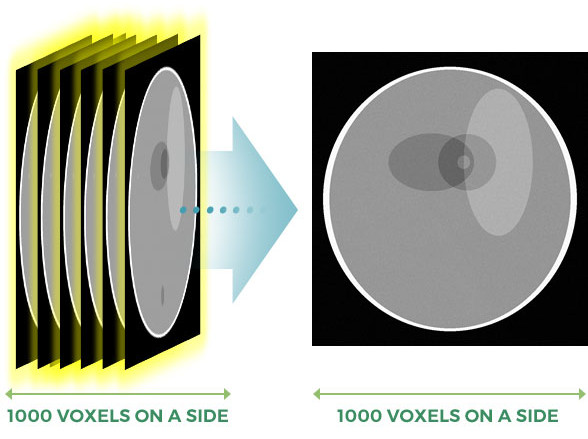
- • 3D Computed Tomography
- • Robotics & Manufacturing
Big Data Problems
CompStor Analytics™ delivers breakthrough run-times
and handles TB sized big data problems robustly
Statistical Machine Learning
and Classification
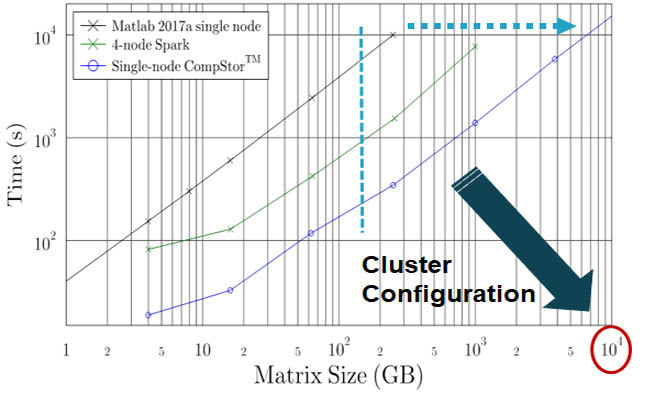
Singular Value Decomposition (SVD)
3-D Tomography with 1B unknowns
and 1.5B equations